¶ Introduction
When flying, the winds create effects on the aircraft trajectory. The winds push the aircraft in the air and the pilot shall compensate this effect in order to land, to perform navigation, to follow radio navigation aid radials or tracks...
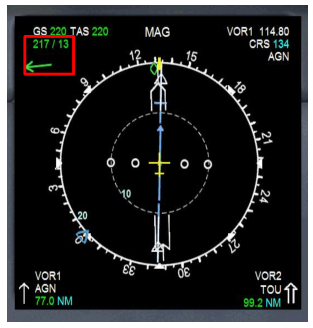
The wind value can be taken from METAR information or can be found on complex navigation instruments.
¶ Headwind, tailwind and crosswind definitions
¶ Headwind
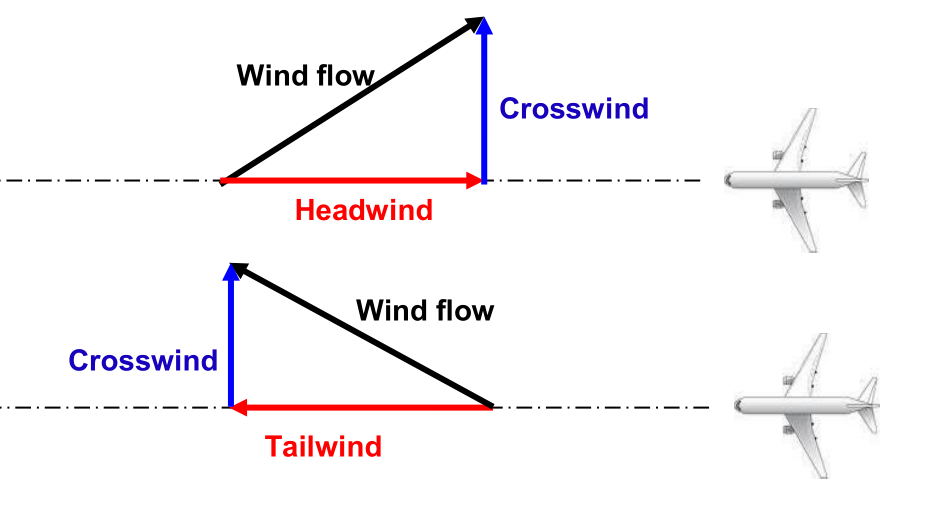
If the winds are pure headwinds, the aircraft will face the wind. The crosswind component is null. The direction of travel is the opposite direction of the wind.

This configuration is the best for landing and taking-off procedures.
¶ Tailwind
If the winds are pure tailwinds, the aircraft will follow the wind. The crosswind component is null. The direction of travel is the same direction of the wind.
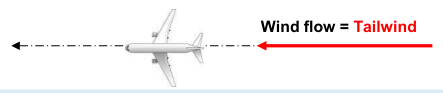
This configuration is the best in en-route phase to save time of travel.
¶ Crosswind
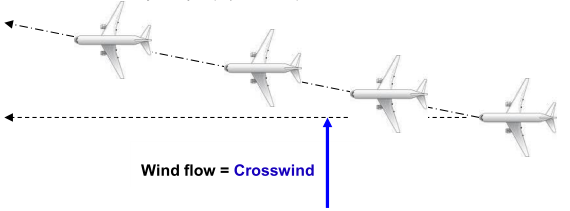
If the winds are pure crosswind, the direction of travel is perpendicular to the wind direction. The headwind and the tailwind are null. The cross wind can be from left to right (like the example below) or from right to left (opposite direction of the example below)
This configuration will not gain time in the en-route phase and will just make the landing a little bit challenging if the crosswind component is sufficiently high.
Crosswind will create trajectory slip (wind will push the aircraft off the desired track.
¶ Generic wind configuration
The wind flow does not follow the runway axis all the time. It often comes from the left or the right.
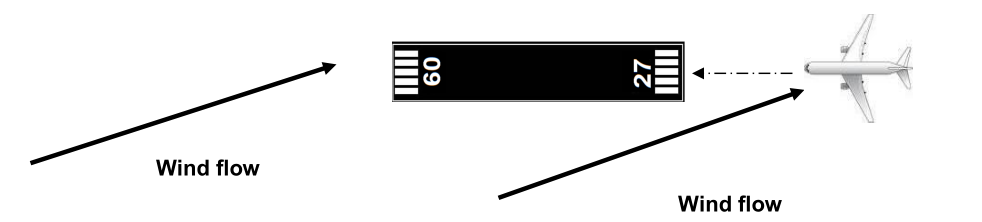
The wind flow can be taken from the METAR information.
There are 2 parts in a wind flow:
- a headwind blows against the direction of travel or a tailwind blows in the same direction of travel
- a cross wind blows using perpendicular direction of travel (from the left or from the right)
¶ Headwind configuration
α is the angle of the wind from direction of travel.
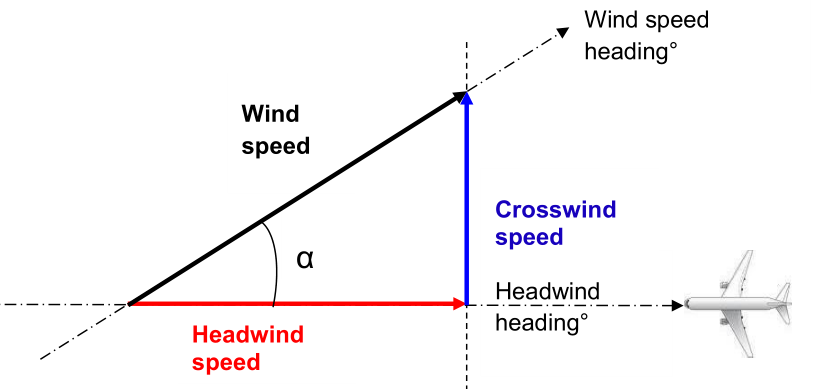
α = (Wind speed heading° - Headwind Heading°)
Headwind heading = Aircraft heading The angle shall be: -90° < α < +90°
Note that METAR heading of the wind is the heading of the aircraft which has the wind in front of him
¶ Tailwind configuration
α is the angle of the wind from direction of travel.
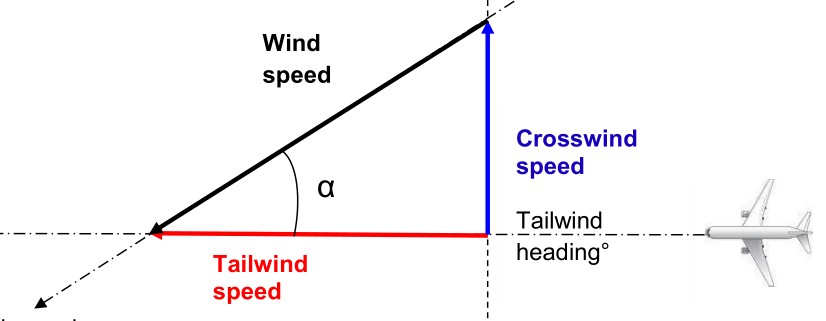
α = (Wind speed heading° - Tailwind Heading°)
Tailwind heading = Aircraft heading + 180 The angle shall be: -90° < α < +90°
¶ Tailwind, headwind and crosswind in function of the runway
Using the same wind, tailwind and crosswind values are different for each runway used! According to the image, the wind direction is coming from the north.
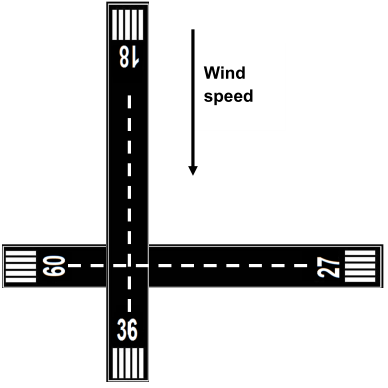
For a take-off, we will have:
- a headwind if aircraft use runway 36
- a tailwind if aircraft use runway 18
- a crosswind from the left if aircraft use runway 09
- a crosswind from the right if aircraft use runway 27
If you have a tailwind for a runway, the opposite runway will have the same wind but in headwind configuration. If you have a headwind for a runway, the opposite runway will have the same wind but in tailwind configuration. If you calculate, the tailwind, headwind and crossing values, you must calculate the values for each runway.
¶ Calculation
We now calculate the crosswind and headwind (tailwind) speeds using the angle α and METAR information:
- Crosswind speed = wind speed × sin ( α )
- Headwind speed (or tailwind) = wind speed × cos ( α )
As the 'sine' and 'cosine' mathematical functions are quite complex, here are some conversion tables:
This table below is the conversion of 'sine' and 'cosine' functions:
| α | 0° | 10° | 20° | 30° | 40° | 50° | 60° | 70° | 80° | 90° |
|---|---|---|---|---|---|---|---|---|---|---|
| sin α | 0 | 0.17 | 0.34 | 0.5 | 0.64 | 0.77 | 0.86 | 0.94 | 0.98 | 1 |
| cos α | 1 | 0.98 | 0.94 | 0.86 | 0.77 | 0.64 | 0.5 | 0.34 | 0.17 | 0 |
We can have a simpler table for wind calculation: here we have approximated crosswind and headwind speeds for a wind speed value = 10kt.
| α | 0° | 10° | 20° | 30° | 40° | 50° | 60° | 70° | 80° | 90° |
|---|---|---|---|---|---|---|---|---|---|---|
| Crosswind (kt) | 0 | 0 | 3 | 5 | 6 | 8 | 9 | 10 | 10 | 10 |
| Tailwind (kt) | 10 | 10 | 9 | 8 | 7 | 6 | 5 | 3 | 0 | 0 |
¶ Example
Input data are:
- Wind speed = 8KT
- Aircraft heading = 60°
- Wind speed heading in METAR = 100°
We are in headwind configuration, so: Headwind = Aircraft heading° = 60° × α = 100° - 60° = 40°
- True mathematical calculation: Crosswind = 8 × sin(40°) = 5.14 KT ; Headwind = 8 × cos(40°) = 6.12 KT
- Calculation with the first table given above: Crosswind = 8 × 0.64 = 5.12 KT ; Headwind = 8 × 0.77 = 6.16 KT : error < 1%
- Calculation with the second table given above: Crosswind = 8 × 6/10 =4.8 KT ; Headwind = 8 × 7/10 = 5.6 KT ; error < 10%
Tailwind and Crosswind values are different for each runway!
For runway 24, if the headwind is +5KT, then for opposite runway 06, the headwind is transformed into a tailwind. So, for the runway 06, Headwind is -5KT or tailwind is +5KT.
- none
- none
- VID 150259 - Creation
- VID 150259 - Wiki integration
- VID 496402 - Wiki.js integration