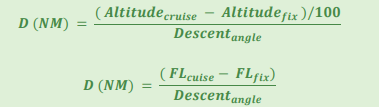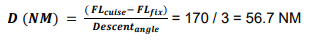¶ Introduction
In aviation, the top of descent, is the computed or calculated point between the cruise or en-route phase and the descent phase of a flight.
In jet liners, the top of descent is usually calculated on-board by the flight management system; this is designed in order to achieve the most economical descent profile to approach altitude, or to meet other requirements (max angle, max rate, etc.).
¶ Top Of Descent calculation
¶ Angle of descent rate
The calculation of descent rate angle says:
TAN( angle°) = descent rate (%)
TAN is a trigonometric function named tangent.
The tangent of an angle is the ratio of the length of the opposite side to the length of the adjacent side
The standard descent is calculated along a 3° descent angle:
TAN(3°) = 0.05240778 ≈ 5.2%
With approximation, as angle value is low, we have the approximation:
- Descent angle (°) ≈ descent rate (%) x 0.6
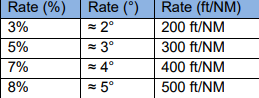
- Rate (ft/NM) ≈ 60 x Rate (%) 1% descent rate = 60ft/NM
- Rate (ft/NM) ≈ 100 x Rate (°) 1° descent angle = 100ft/NM
With previous equation, we can compute this table:
¶ Rule of 3
In aviation and based on a 3° descent rate, transport pilots adopted a formula to assure a slow, steady and comfortable descent for their passengers: the rule of three or "3:1 rule of descent".
This rule implies 3 NM of travel should be allowed for every 1,000 feet (300 m) of descent.
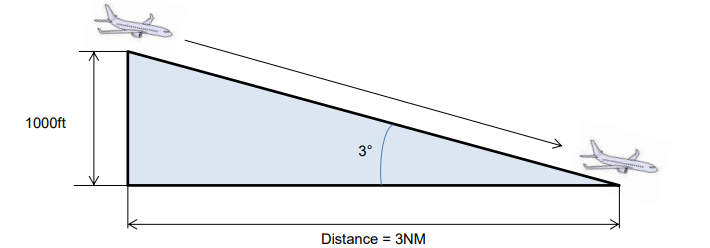
The "rule of 3" is used by pilots flying small aircraft as well as by those flying airliners.
This descent gives an efficient glide descent from cruising altitude. The standard descent speed will be
close to (usually slightly higher than) the optimum Lift/Drag ratio speed, and will give a descent ratio close
to 3:1.
¶ Top of Descent - TOD
The top of descent or TOD is the point for an aircraft to initiate a descent to a lower lever for arrival at the destination airfield. The aircraft is leaving the cruise phase of the flight and start a descent phase to thefirst approach altitude expected at one approach fix.
The top of descent is usually calculated by an on-board flight management system, and is designed to provide the most economical descent to the approach altitude.
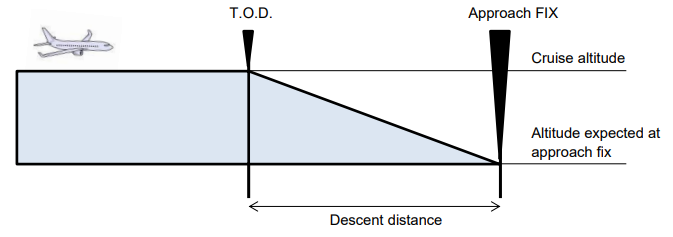
This diagram is also applicable for VFR flights. You can replace the approach fix by a VFR entry point, landmark or over airfield altitude.
¶ Start of descent distance from fix
The start of descent distance is calculated using this formula:
D: start of descent distance before expected approach fix (NM)
Altitude cruise: cruise altitude (ft)
Altitude fix: altitude expected at approach fix (ft)
FL cruise: cruise flight level
FL Fix: flight level expected reaching fix point wanted
Descent Angle: descent angle chosen (°)
Example:
We are flying at 33.000ft/FL330
We need to descent to the next point at 12.000ft/FL120 at standard commercial rate 3°.
D (NM) = (330-120) / 3° = 210/3 = 70 NM
Result is that we shall start the descent 70NM before the approach point.
In order to have margin in descent, it is recommended to add 1NM up to 5NM to this calculated distancedue to the descent rate establishment and winds effect.
¶ Descent rate calculation
The top of descent is now known, but pilots should be able to know which descent rate in feet per minute to select in their cockpit or monitor in their instrument.
Descent rate using the Ground speed approximation formula:
Vertical speed (ft/min) = Descent rate (%) x Ground speed (knots)
Example:
Ground speed is 110kt, and descent rate is standard 5.2%.
Note that the descent rate value can be approximated using only 5% instead of 5.2%.
Vertical speed = 5 x 110 = 550ft/min,
(if we use 5.2% instead, vertical speed will be 572 ft/min = less than 5% error).
But this formula has some restrictions:
- Ground speed in some aircraft is not known because the wind is not known
- Ground speed can change during descent if this speed is not maintained constant.
As first approximation, GS can be replaced by TAS if known or an approximation of TAS:
- If the TAS can be maintained constant, in this way, by using a constant vertical speed, we will remain at the same descent rate during the descent.
- If the TAS cannot be maintained constant, if we want to remain at the same descent rate, we shall adjust in permanence the descent rate. As the TAS is decreasing when the altitude decreases, the vertical speed shall be decreased and adjusted using the same formula.
For high altitude and speed above 250KT, we can take the approximation of True air speed:
TAS = IAS + FL/2
Vertical speed (ft/min) = Descent rate (%) x Ground speed (knots) = Descent rate x (IAS + FL/2)
The flight level taken can be at the middle between the cruise flight level and the expected final flight level in order to compensate for the decrease of TAS.
Example:
I am flying at FL300 and we shall be at the initial approach fix at FL110.
Our IAS during descent shall be 300KT. We will take FL200 for the compensation of TAS decreasing:
Vertical speed (ft/min) = 5 x (300 + 200/2) = 5 x400 = 2000ft/min
¶ Descent rate using Mach number
At high altitude above FL260, the commercial aircraft are flying during the cruise phase using a constant Mach number independent of the altitude chosen by the pilot.
The pilot can initiate also a first phase of descent using a constant Mach number:
Vertical speed (ft/min) = Descent angle (°) x Mach x 1000
Example:
MACH is 0.80, and descent angle is standard 3°
Vertical speed = 3 x 0.80 x 1000 = 2.4 x 1000 = 2400ft/min
¶ Descent with constant descent rate
Descent could be started when the time to reach the point is equal to lose multiple of 1000ft/min descent.
If we are expecting to reach the final approach fix at about 20 minutes and we are flying at 20.000ft, we can start our descent at 1000ft/min in case that we are not expecting any altitude restrictions.
If we are expecting to reach the final approach fix at about 10 minutes and we are flying at 30.000ft, we can start our descent at 3000ft/min in case that we are not expecting any altitude restrictions.
It is important to know that sometimes, speed and altitude restrictions shall be applied at our flights.
Using a too high descent rate, an aircraft may not respect the speed and altitude constraints published on charts, established by regulations or given by ATC.
¶ Practical example
Data:
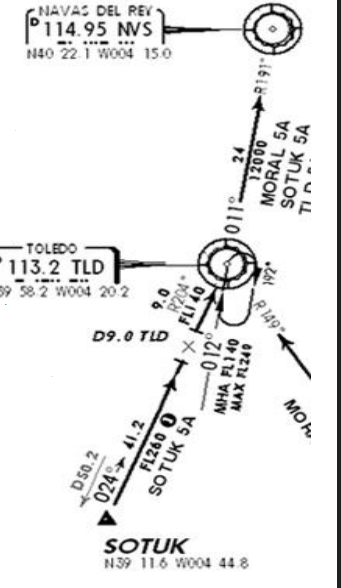
We are expecting to perform the SOTUK5A arrival. Our last enroute way point is SOTUK.
We are supposed to overfly the TLD (TOLEDO) VOR at FL210 (maximum)
Currently, our aircraft is on cruise flight level FL380 at more than 50NM inbound SOTUK at 450KT ground
speed.
Question:
What is the distance of TOD before joining SOTUK ?
We take the standard descent consideration (1000ft x 3nm), from FL380 to FL210, We expect 17000ft
vertical altitude loss:
The descent shall start 56.7NM from TLD.
If we follow the chart, the distance between SOTUK and TLD is 50.2 NM.
We will program our descent 56.7-50.2 = 6.5 NM before the fix SOTUK.
We will calculate the required vertical speed to achieve the 3º descent angle:
Vertical speed = 5 x GS = 5 x 450 = 2250 ft/min.
As we expect 5.2% for optimal calculation, we will choose approximation 2300ft/min
At SOTUK, we notice that the ground speed is falling down to 410KT.
(Due to wind direction change for example)
We shall calculate a new vertical speed to maintain the 3° descent angle:
Vertical speed = 5 x GS = 5 x 410 = 2050 ft/min.
We will choose approximation 2100ft/min.
On the autopilot, we shall decrease the rate down to 2100ft/min
- None
- None
- VID 150259 - Creation
- VID 489972 - Wiki.js Integration